三角形和圓的面積

很早就想分享這篇文章的內容了。不知道大家以前上數學課的有沒有這種感受：

老師正在講：

橡皮擦掉了，我撿起來就看見是這樣的了：

從此我的數學課就一直沒有聽懂過。

今天我和大家分享下我整理的兩個求圖形面積的公式，分別是三角形和圓。

三角形的面積

首先，我們都知道長方形的面積是： S = h * w。

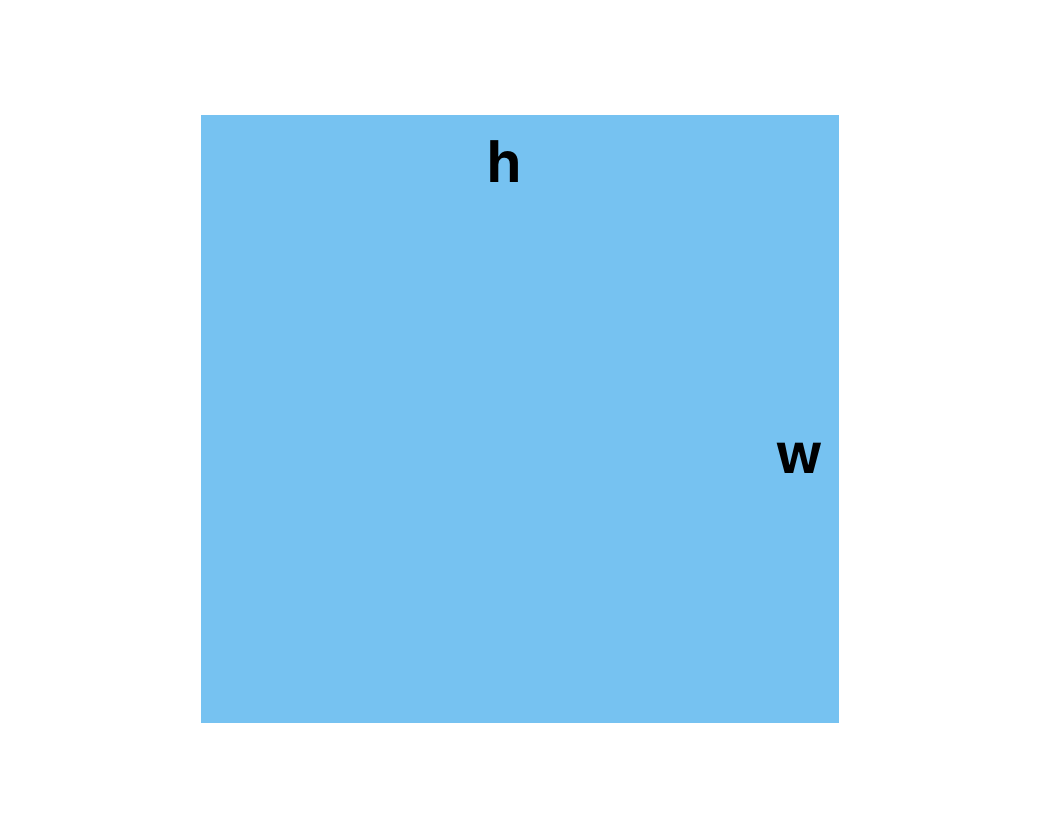
然後我被告知三角形的面積是：S = h * w / 2。老師怎麽說，我就怎麽做，這麽多年就這樣過來了，但是我沒有去深刻認識這些東西到底為什麽是這樣，多年以後，從不同的角度思考後，我想我是理解了，從本質上去認識到了這其中的原因。

這裏不涉及諸如兩個三角形疊加組成四邊形那種算法，我們這裏說說另外一種積分的，涉及到抽象角度的無窮這個概念。

這是一個三角形：

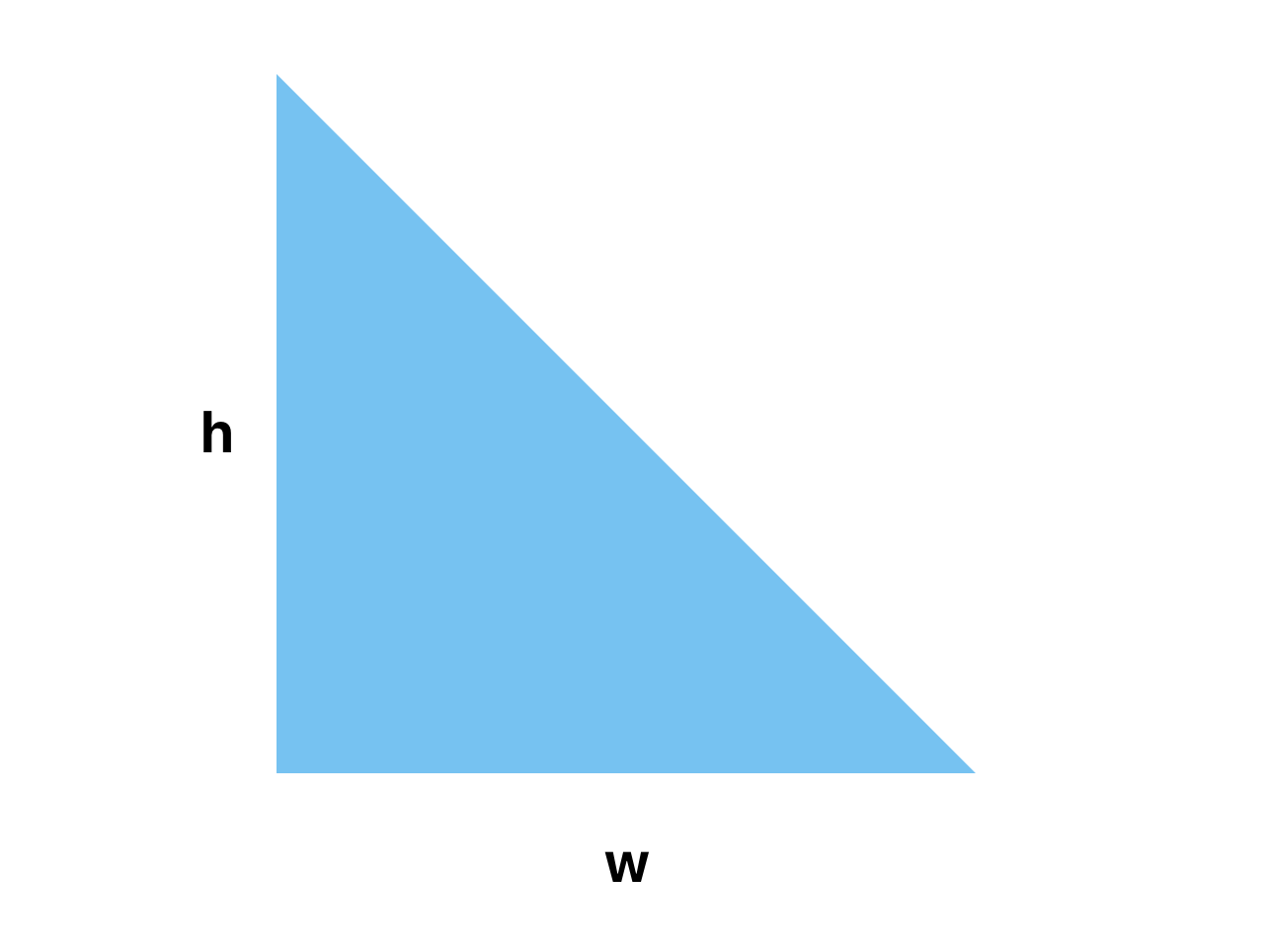
我們按照等寬截取出一個個的小長方形，想想，只要我們的截取的寬度足夠小，那麽最後這些小長方形的面積之和就等於這個三角形的面積：

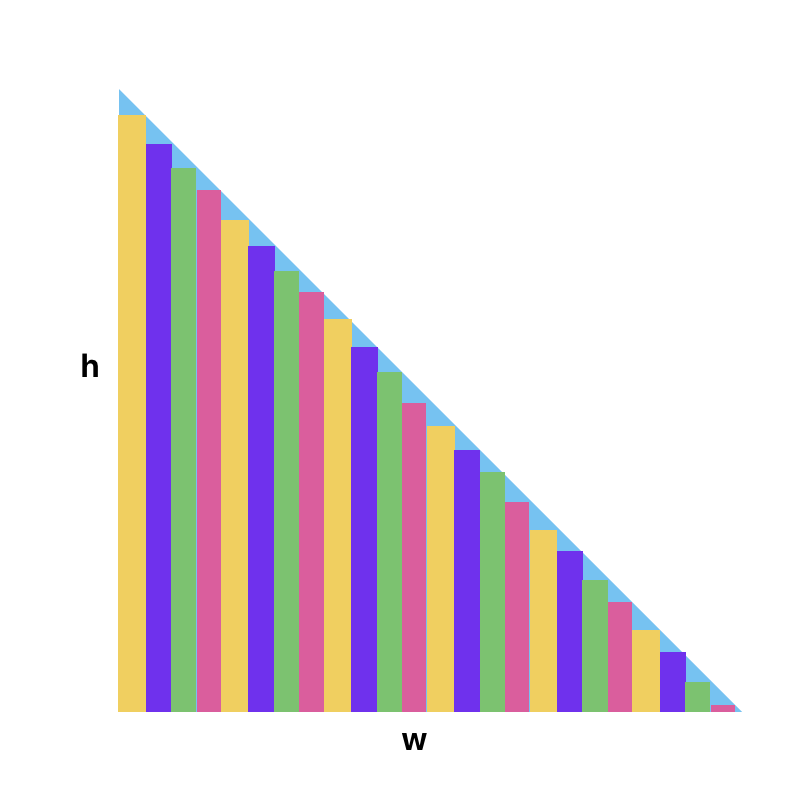
我們這裏對寬做個等分處理，分成n份：

高度也劃分為n等份，每個右邊的長方形比左方的少 h / n, 我們這裏賦值給 Δh = h / n ：

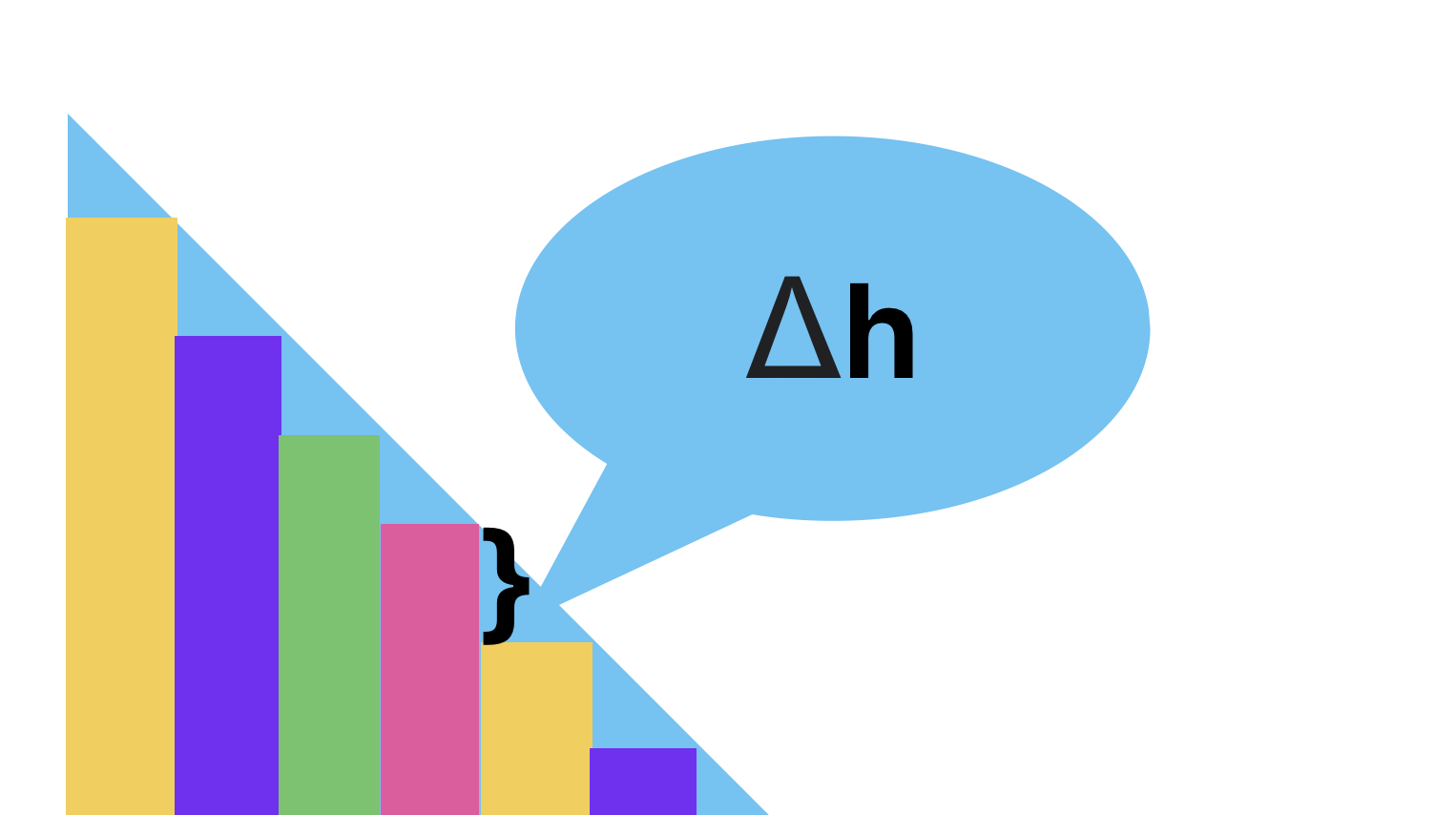
那麽現在我們來推算：

• 第一個長方形的面積就是：S = w/n * h;
• 第二個長方形的面積就是：S = w/n * (h - Δh);
• 第三個長方形的面積就是：S = w/n * (h - Δh * 2);
• …
• 第n個長方形的面積就是：S = w/n * (h - Δh * (n-1));

我們對他們求和：

S = w/n * h + w/n * (h - Δh) + … + w/n * (h - Δh * (n-1))

S = w/n * (h + (h - Δh)+ … + (h - Δh * (n-1)))

S = w/n * (h * n - Δh * (1 + 2 + … + (n-1)))

S = w/n * (h * n - Δh * n * n/2)

按照我們之前對高的劃分： h = Δh * n，我們可以繼續推導出：

S = w/n * (h * n - h * n/2)

S = w/n * h * n/2

S = w * h /2

就此我們得出三角形的面積 S = w * h /2 。

是不是挺有趣的，我們繼續。

圓的周長

在說圓的面積之前，我們先說說周長。

我不知道你們有沒有這樣做過，反正我是真試過，用圓規在紙上畫一個圓，然後把圓從紙上剪下來，用卷尺量它的周長，最後發現周長確實是半徑的6倍左右，如果你畫的圓越大，越精確，你肯定可以得到更精準的倍數。

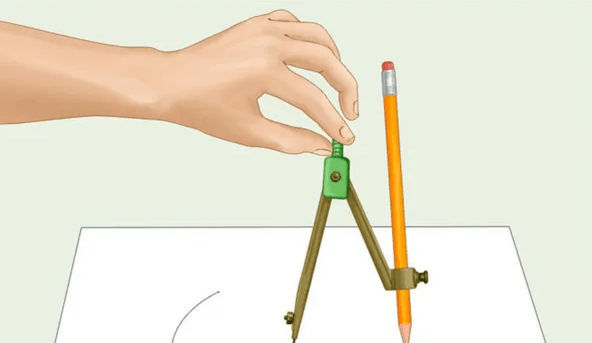
我們都知道圓的周長公式是：C = 2 * π * r，這個是可以通過我上邊說的方法實踐發現的。

圓的面積

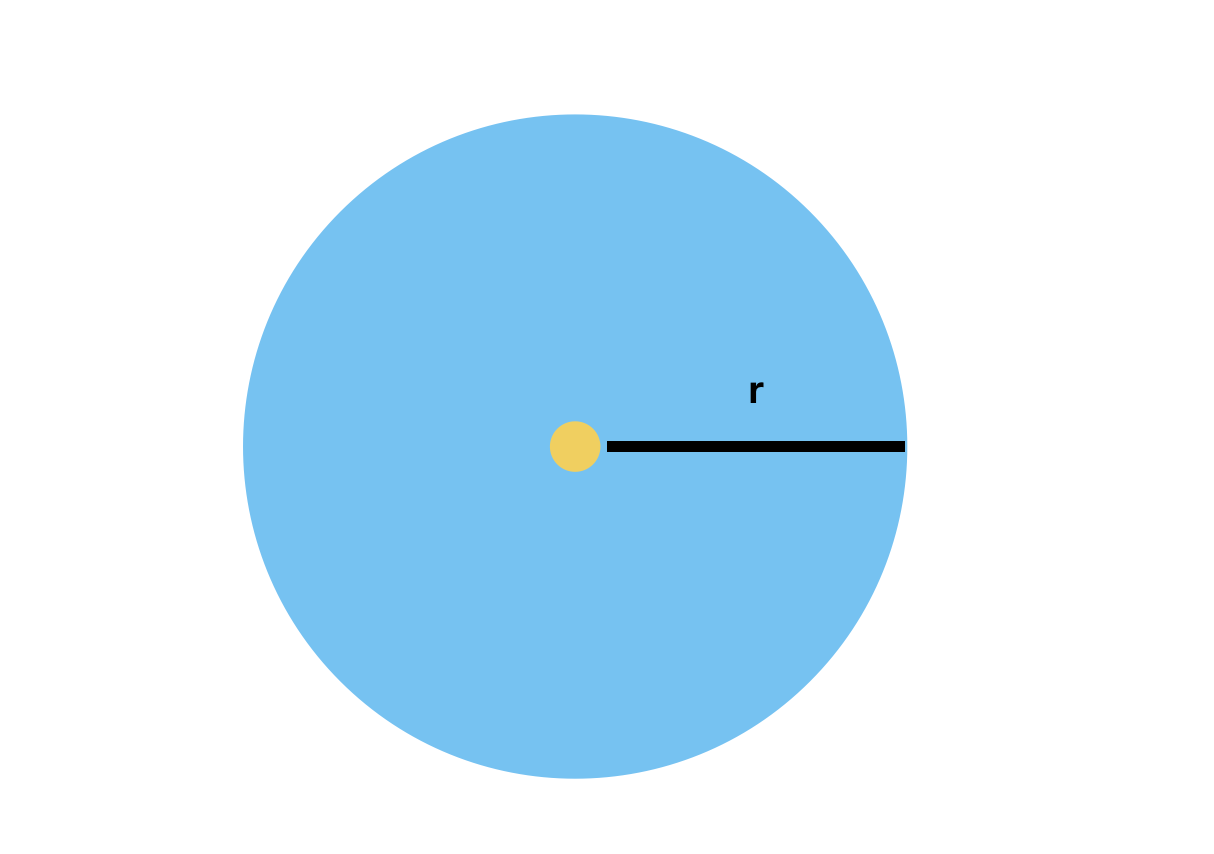
延用我們用的算三角形的面積的方法，我們把圓劃分為一條條的彩帶，就像這樣：

我們把這些帶子提取出來，排列好，就類似這樣：

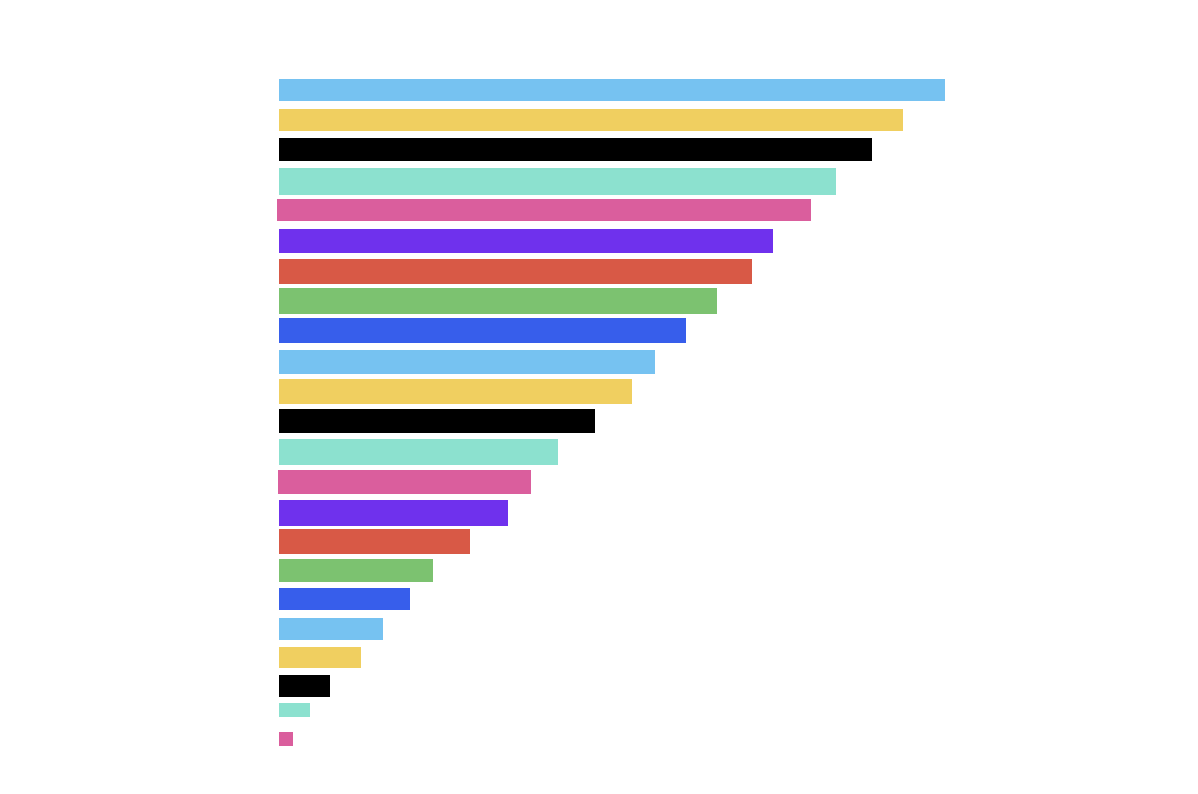
看到這裏有沒有覺得眼熟，是不是又變成一個三角形了。

我們也是把圓分成寬度相等的n份，那麽每條帶子的寬度就是 r / n.

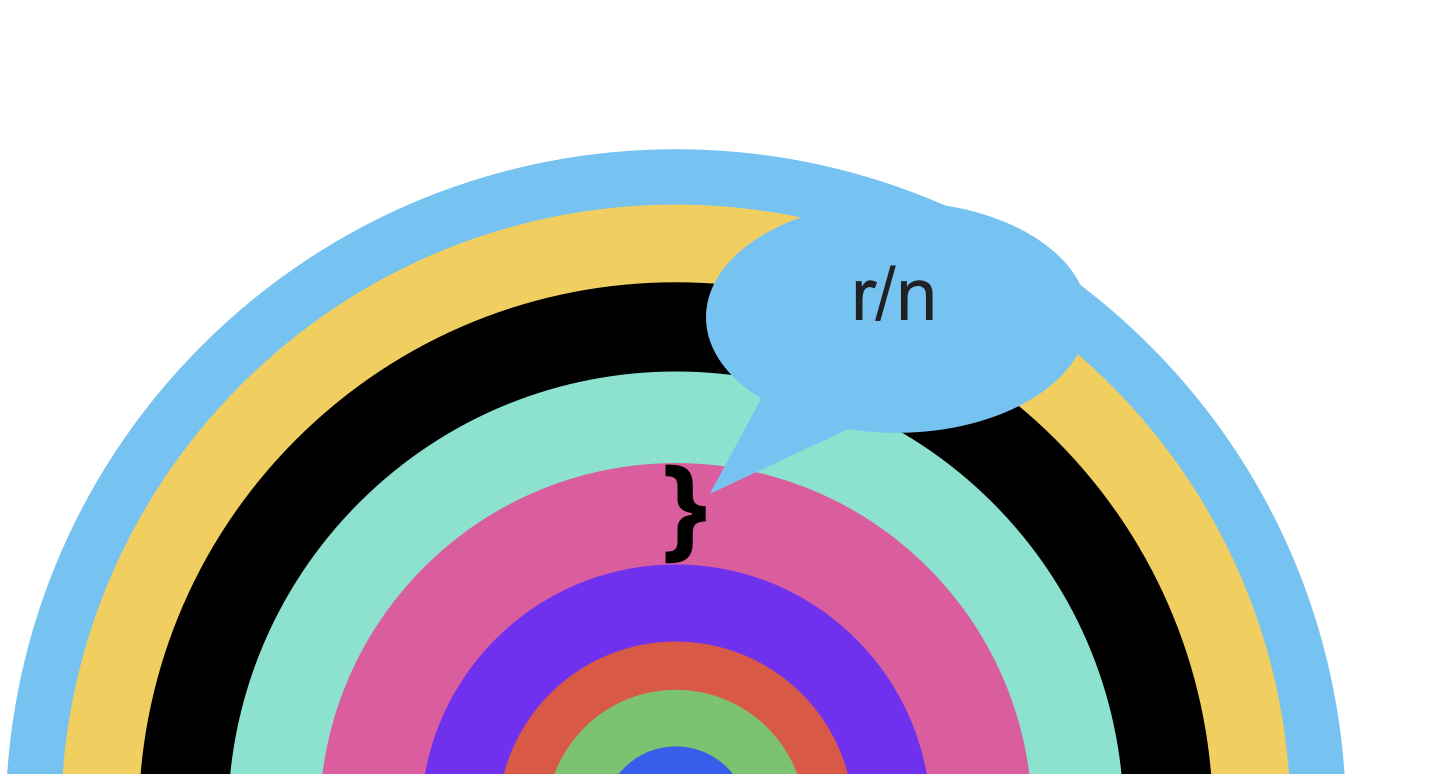
最外圍的帶子長度就是圓的周長，也就是 C = 2 * π * r。換成三角形的話就對應小長方形的高度 h，而每份帶子的寬度是 r / n，那麽所有帶子的總寬度就是 r。

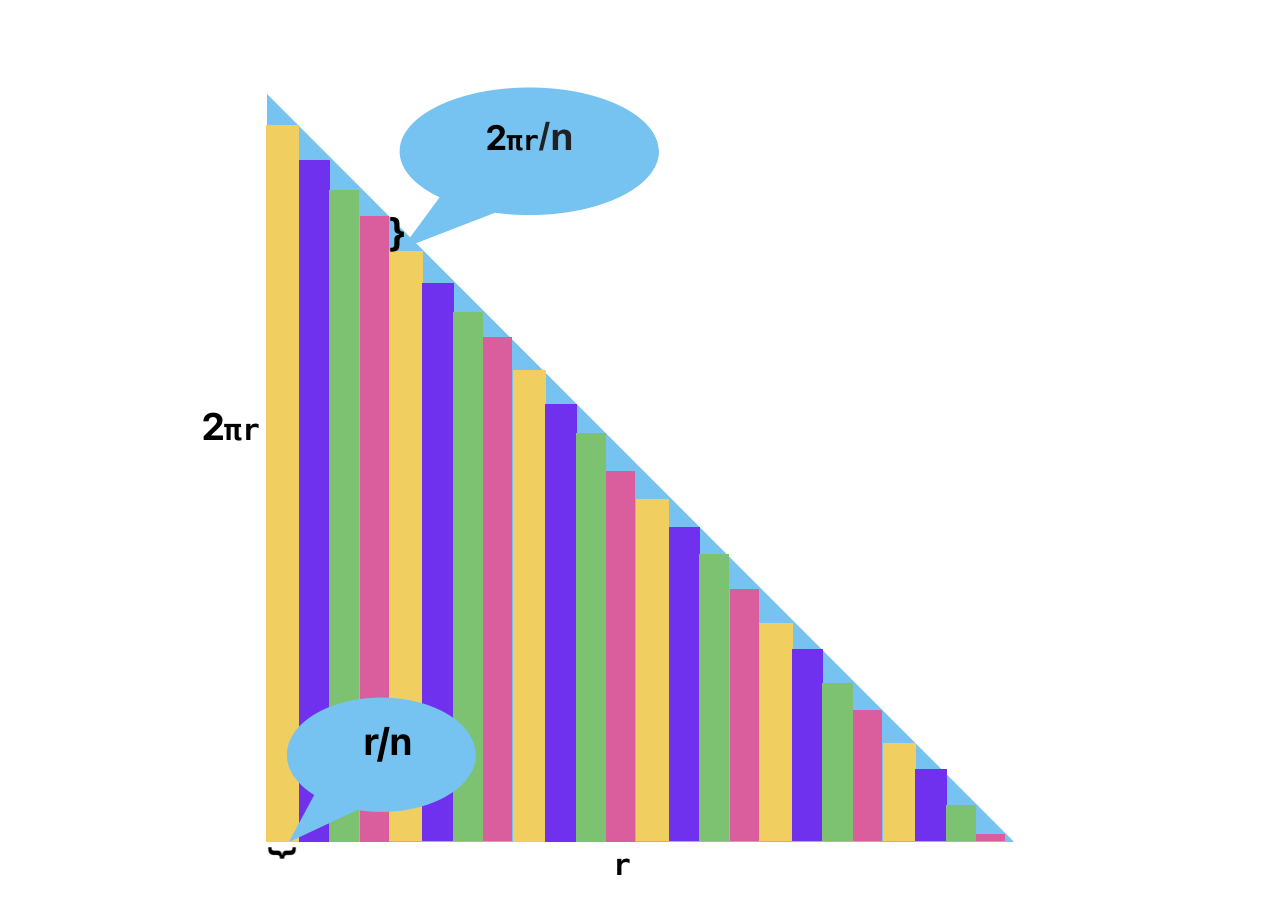
那麽既然是個三角形了，我們就按照三角形的面積計算公式來算：S = w * h /2

S = w * h /2

S = r * (2 * π * r) /2

S = π * r * r

就此我們也算出了圓的面積，是不是非常有趣。

這篇文章就先分享這麽多，我們後邊繼續。