三角形和圆的面积

很早就想分享这篇文章的内容了。不知道大家以前上数学课的有没有这种感受：

老师正在讲：

橡皮擦掉了，我捡起来就看见是这样的了：

从此我的数学课就一直没有听懂过。

今天我和大家分享下我整理的两个求图形面积的公式，分别是三角形和圆。

三角形的面积

首先，我们都知道长方形的面积是： S = h * w。

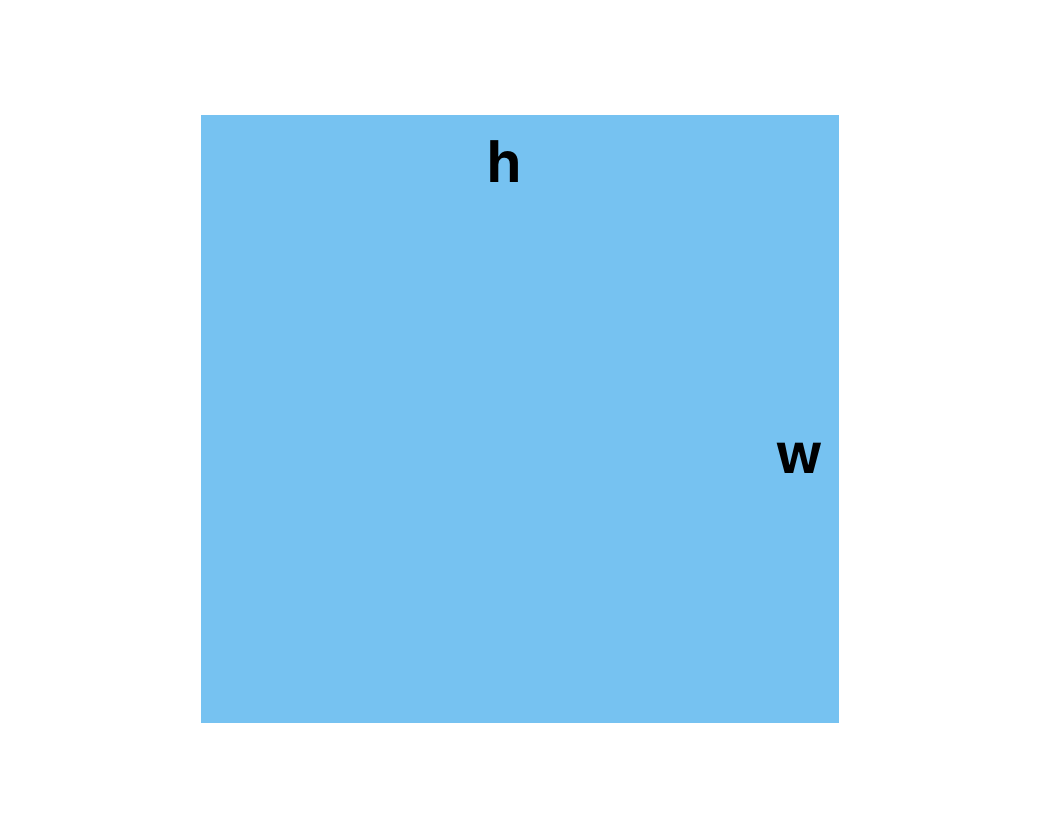
然后我被告知三角形的面积是：S = h * w / 2。老师怎么说，我就怎么做，这么多年就这样过来了，但是我没有去深刻认识这些东西到底为什么是这样，多年以后，从不同的角度思考后，我想我是理解了，从本质上去认识到了这其中的原因。

这里不涉及诸如两个三角形叠加组成四边形那种算法，我们这里说说另外一种积分的，涉及到抽象角度的无穷这个概念。

这是一个三角形：

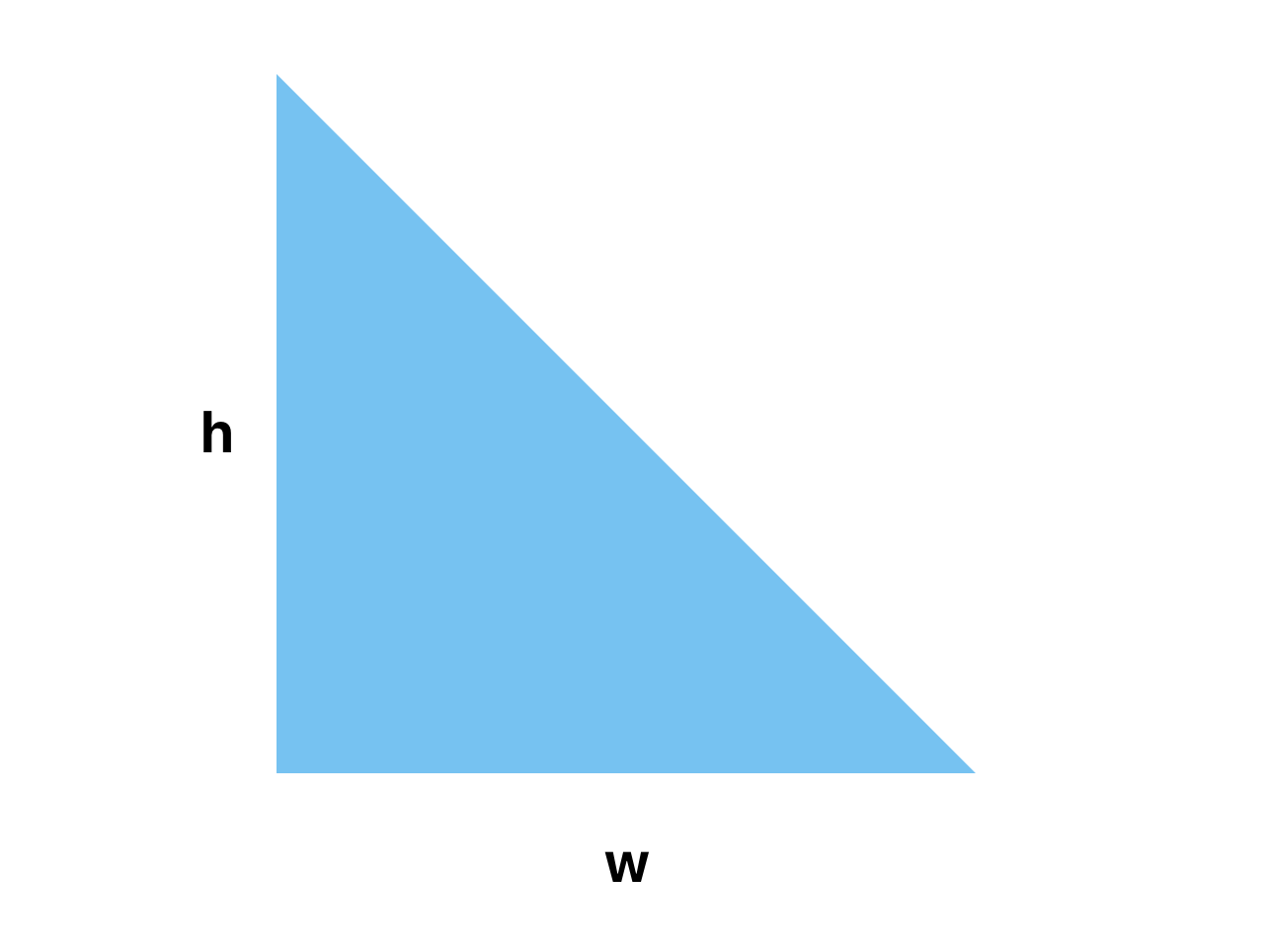
我们按照等宽截取出一个个的小长方形，想想，只要我们的截取的宽度足够小，那么最后这些小长方形的面积之和就等于这个三角形的面积：

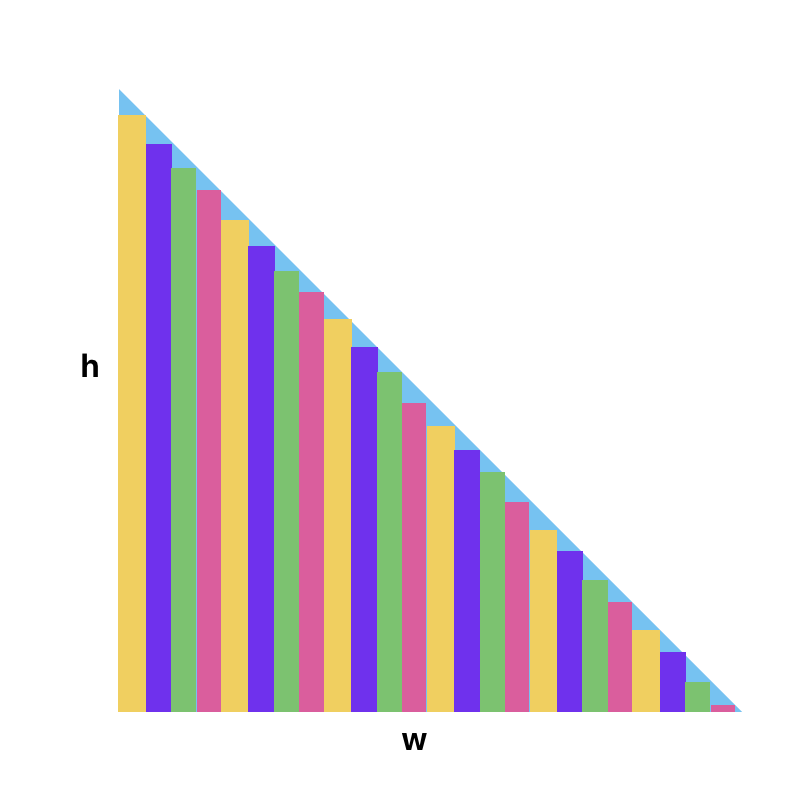
我们这里对宽做个等分处理，分成n份：

高度也划分为n等份，每个右边的长方形比左方的少 h / n, 我们这里赋值给 Δh = h / n ：

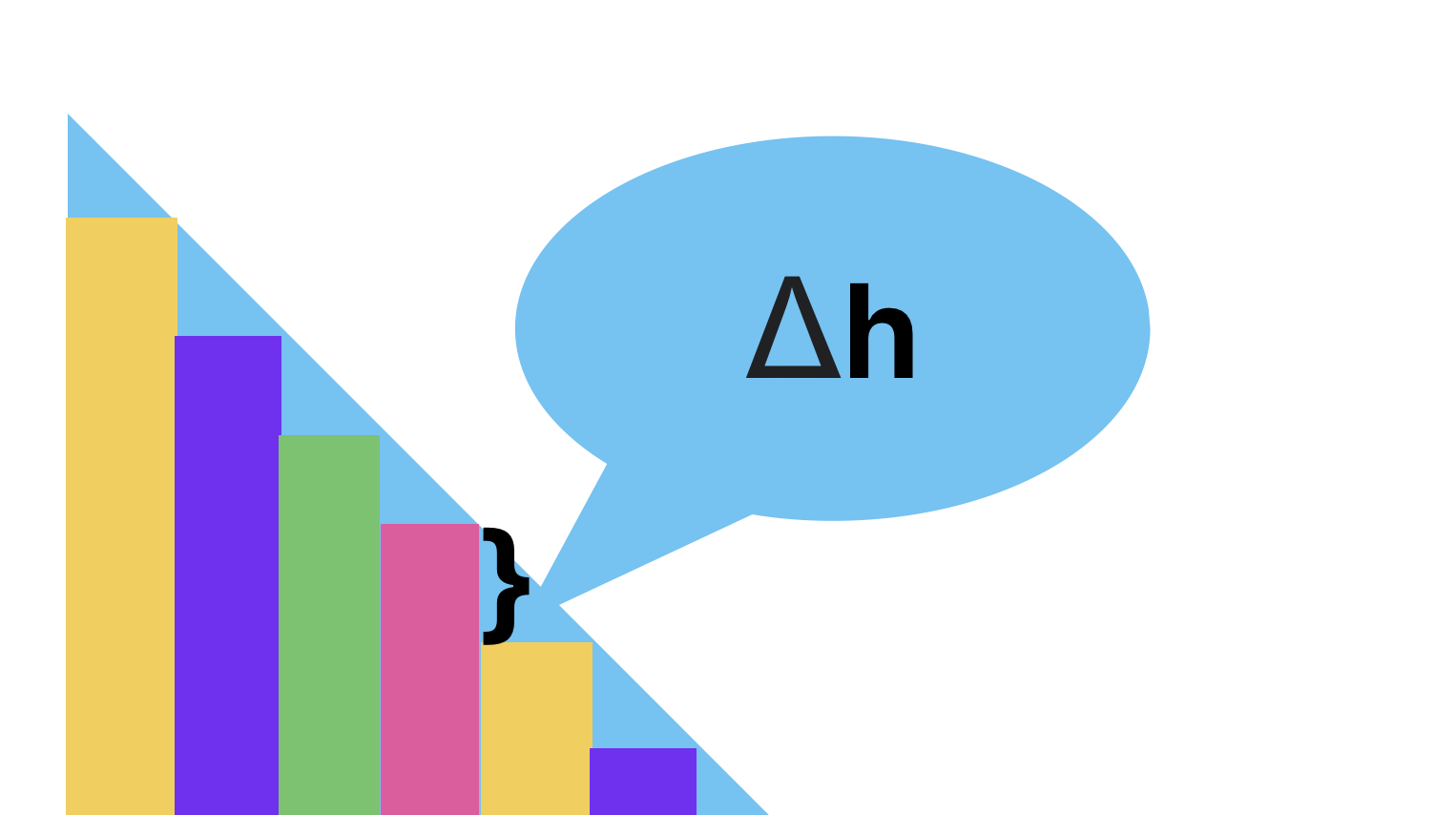
那么现在我们来推算：

• 第一个长方形的面积就是：S = w/n * h;
• 第二个长方形的面积就是：S = w/n * (h - Δh);
• 第三个长方形的面积就是：S = w/n * (h - Δh * 2);
• …
• 第n个长方形的面积就是：S = w/n * (h - Δh * (n-1));

我们对他们求和：

S = w/n * h + w/n * (h - Δh) + … + w/n * (h - Δh * (n-1))

S = w/n * (h + (h - Δh)+ … + (h - Δh * (n-1)))

S = w/n * (h * n - Δh * (1 + 2 + … + (n-1)))

S = w/n * (h * n - Δh * n * n/2)

按照我们之前对高的划分： h = Δh * n，我们可以继续推导出：

S = w/n * (h * n - h * n/2)

S = w/n * h * n/2

S = w * h /2

就此我们得出三角形的面积 S = w * h /2 。

是不是挺有趣的，我们继续。

圆的周长

在说圆的面积之前，我们先说说周长。

我不知道你们有没有这样做过，反正我是真试过，用圆规在纸上画一个圆，然后把圆从纸上剪下来，用卷尺量它的周长，最后发现周长确实是半径的6倍左右，如果你画的圆越大，越精确，你肯定可以得到更精准的倍数。

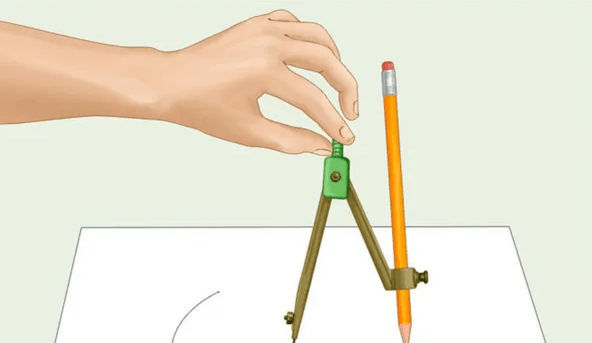
我们都知道圆的周长公式是：C = 2 * π * r，这个是可以通过我上边说的方法实践发现的。

圆的面积

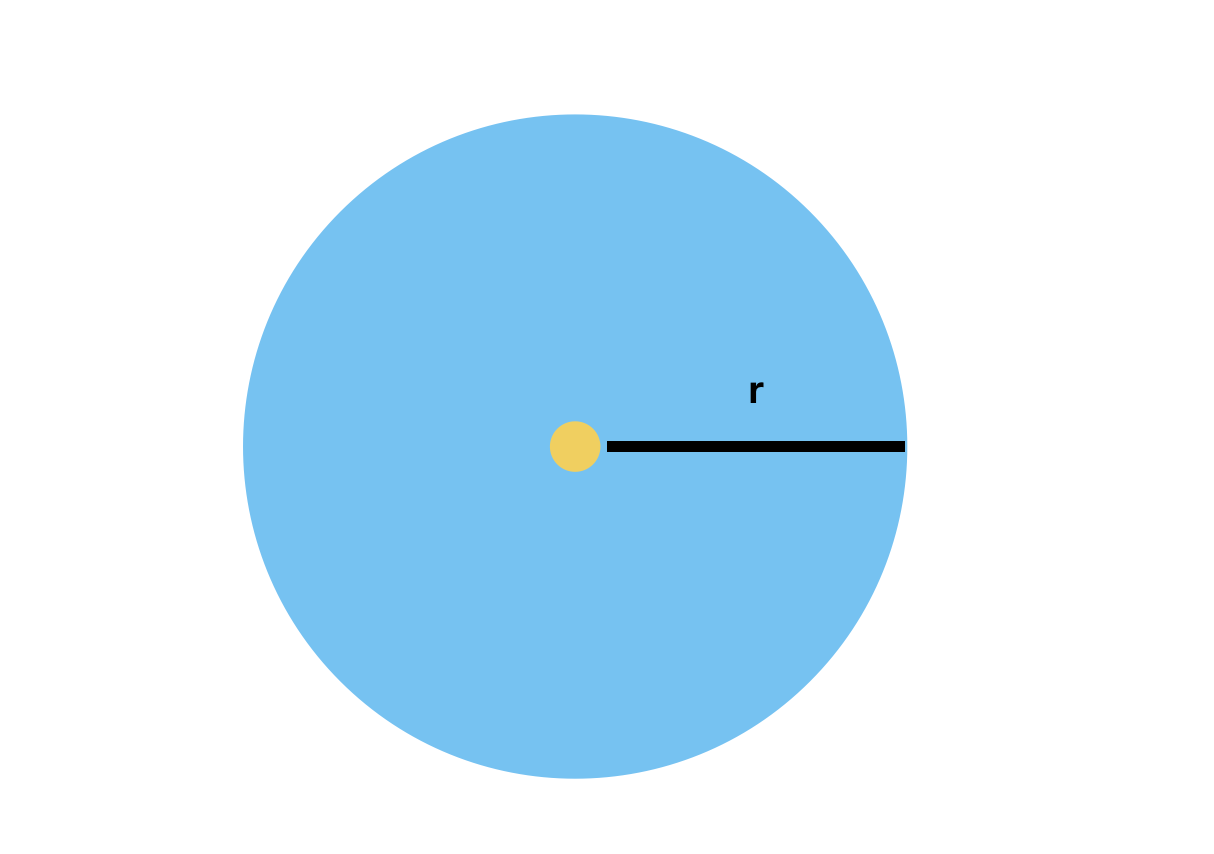
延用我们用的算三角形的面积的方法，我们把圆划分为一条条的彩带，就像这样：

我们把这些带子提取出来，排列好，就类似这样：

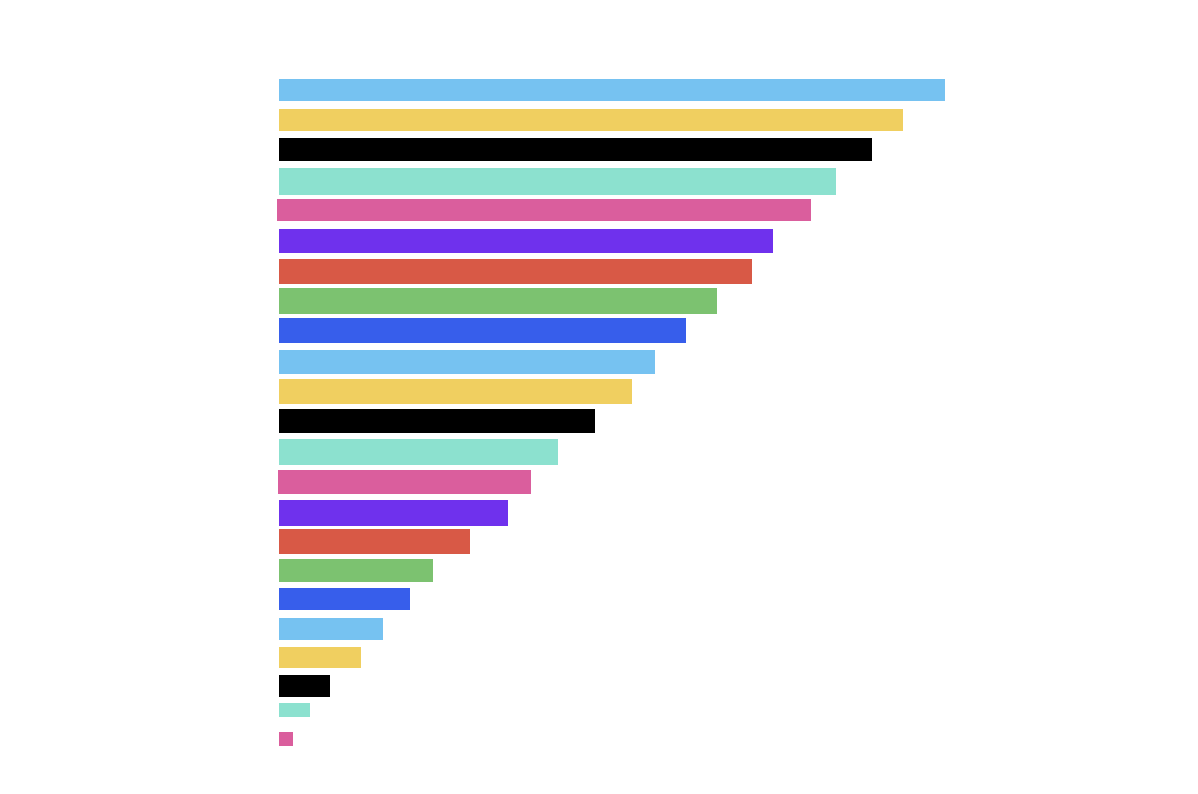
看到这里有没有觉得眼熟，是不是又变成一个三角形了。

我们也是把圆分成宽度相等的n份，那么每条带子的宽度就是 r / n.

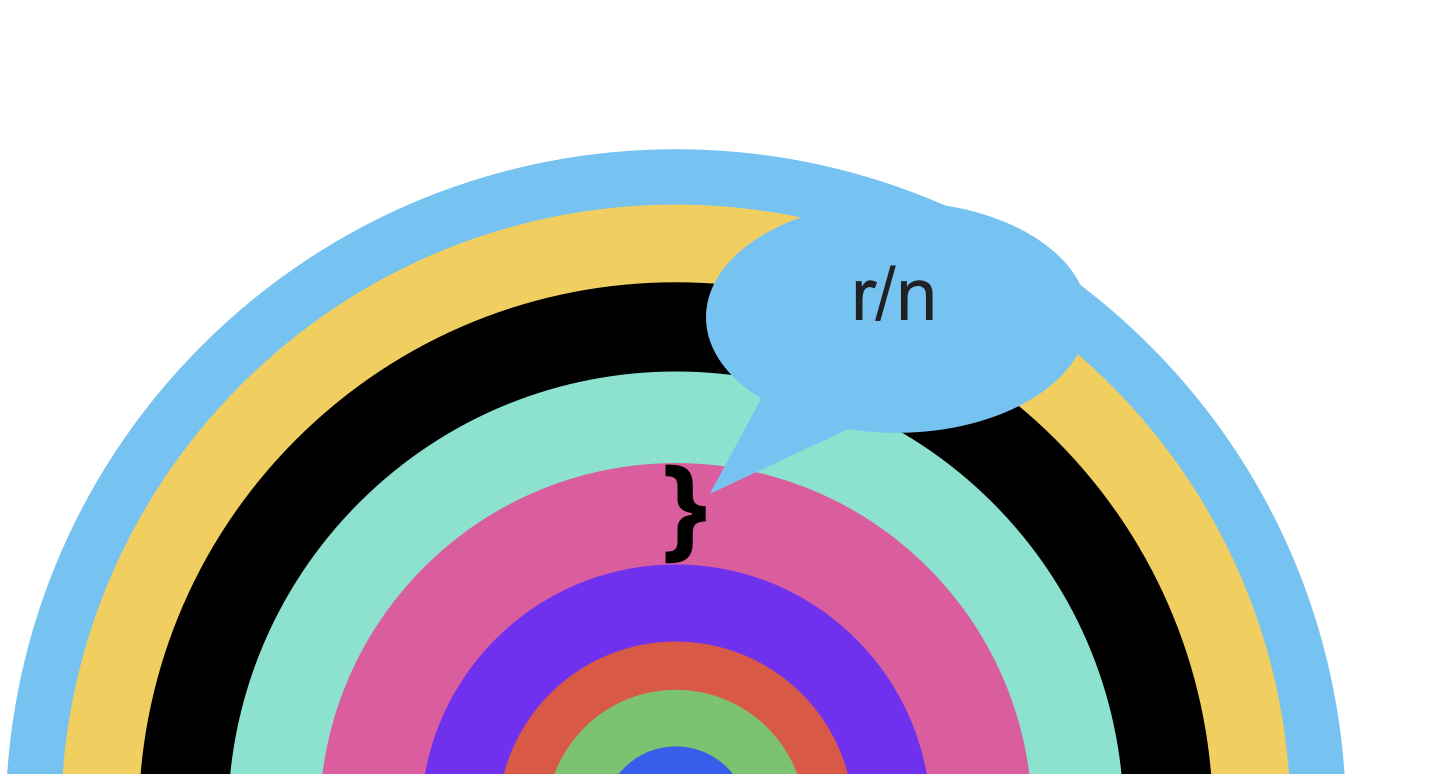
最外围的带子长度就是圆的周长，也就是 C = 2 * π * r。换成三角形的话就对应小长方形的高度 h，而每份带子的宽度是 r / n，那么所有带子的总宽度就是 r。

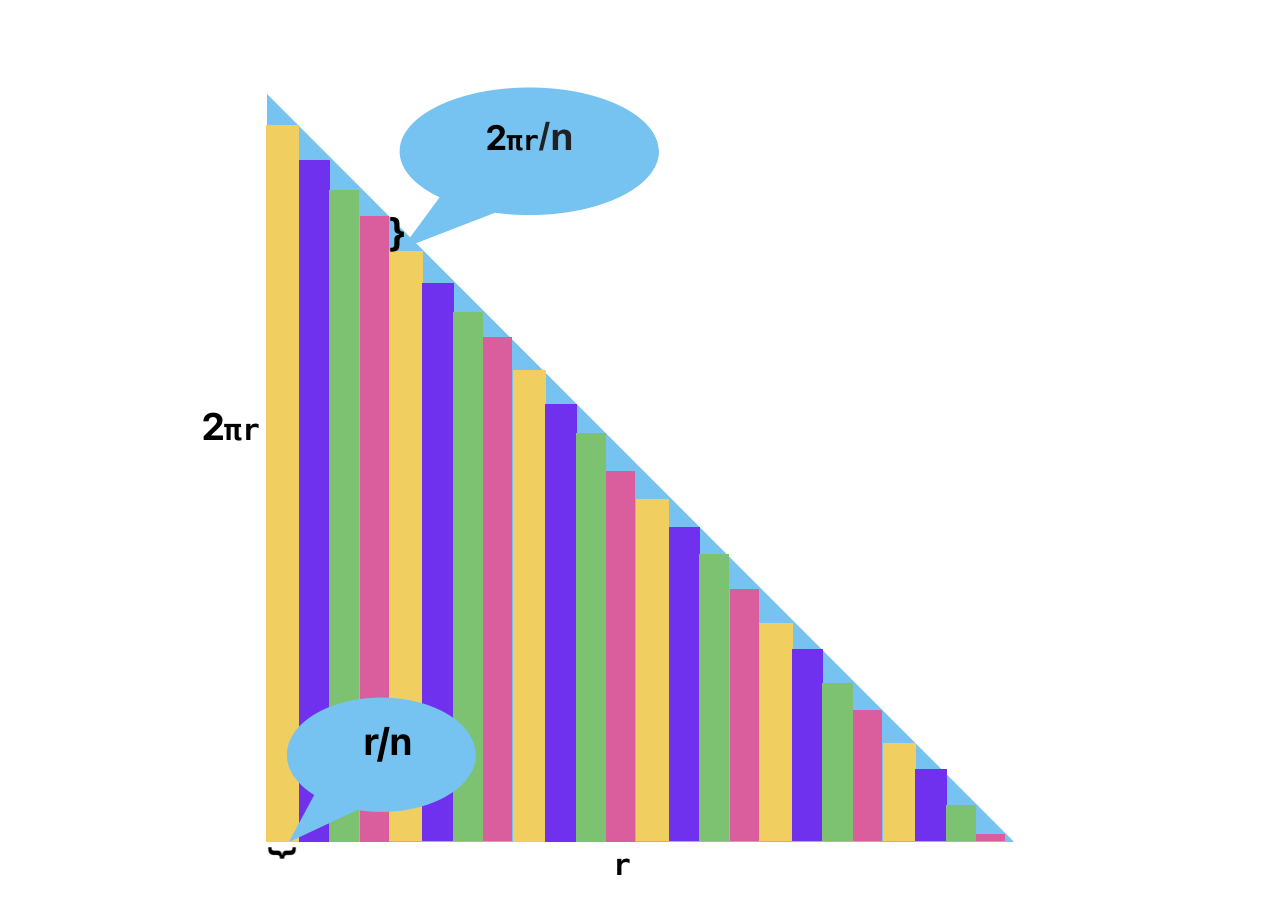
那么既然是个三角形了，我们就按照三角形的面积计算公式来算：S = w * h /2

S = w * h /2

S = r * (2 * π * r) /2

S = π * r * r

就此我们也算出了圆的面积，是不是非常有趣。

这篇文章就先分享这么多，我们后边继续。