Areas of Triangles and Circles

I’ve been wanting to share this content for a long time. I wonder if any of you had the same experience in math class:

The teacher was explaining:

But then my eraser fell, and when I picked it up, this is what I saw:

From that moment on, I never understood math class.

Today, I want to share with you two formulas for finding the area of shapes: triangles and circles.

Area of a Triangle

First, we all know that the area of a rectangle is given by: S = h * w.

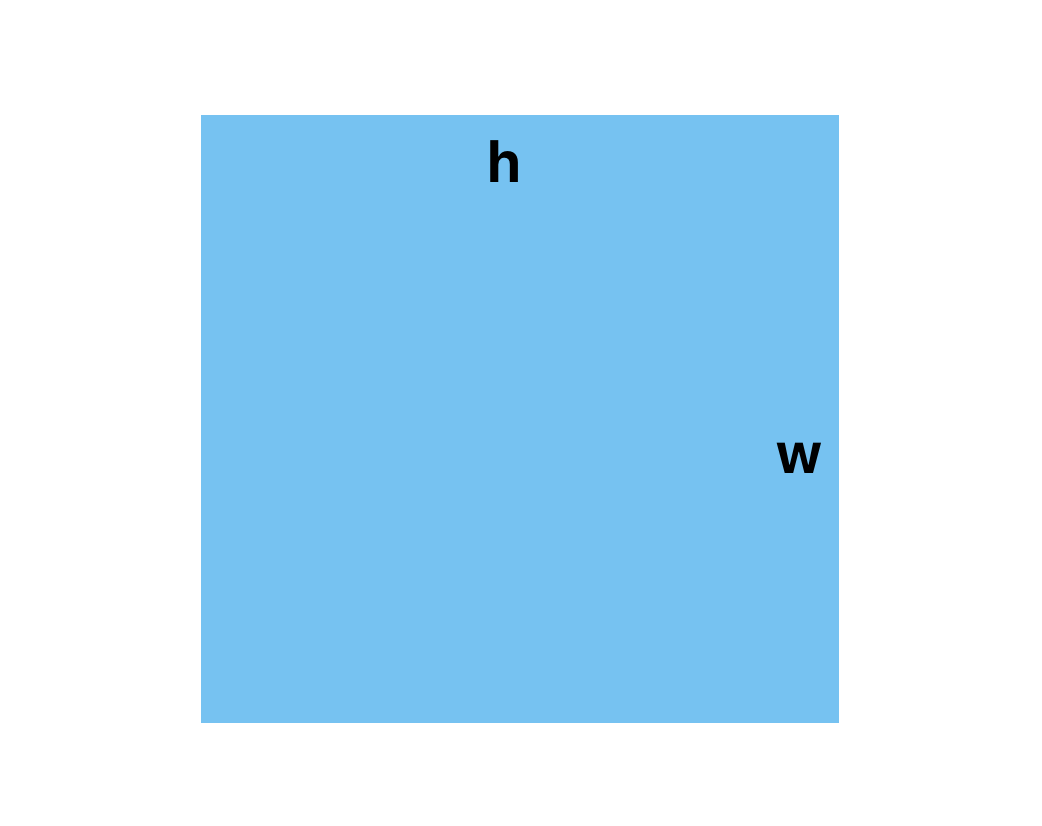
Then I was told that the area of a triangle is: S = h * w / 2. I followed what the teacher said for many years without questioning why it was so. However, after thinking about it from different perspectives over the years, I think I’ve come to understand the fundamental reasoning behind it.

Here, we won’t discuss the method of combining two triangles to form a quadrilateral. Instead, we’ll explore an alternative approach using integration, involving the abstract concept of infinity.

Let’s start with a triangle:

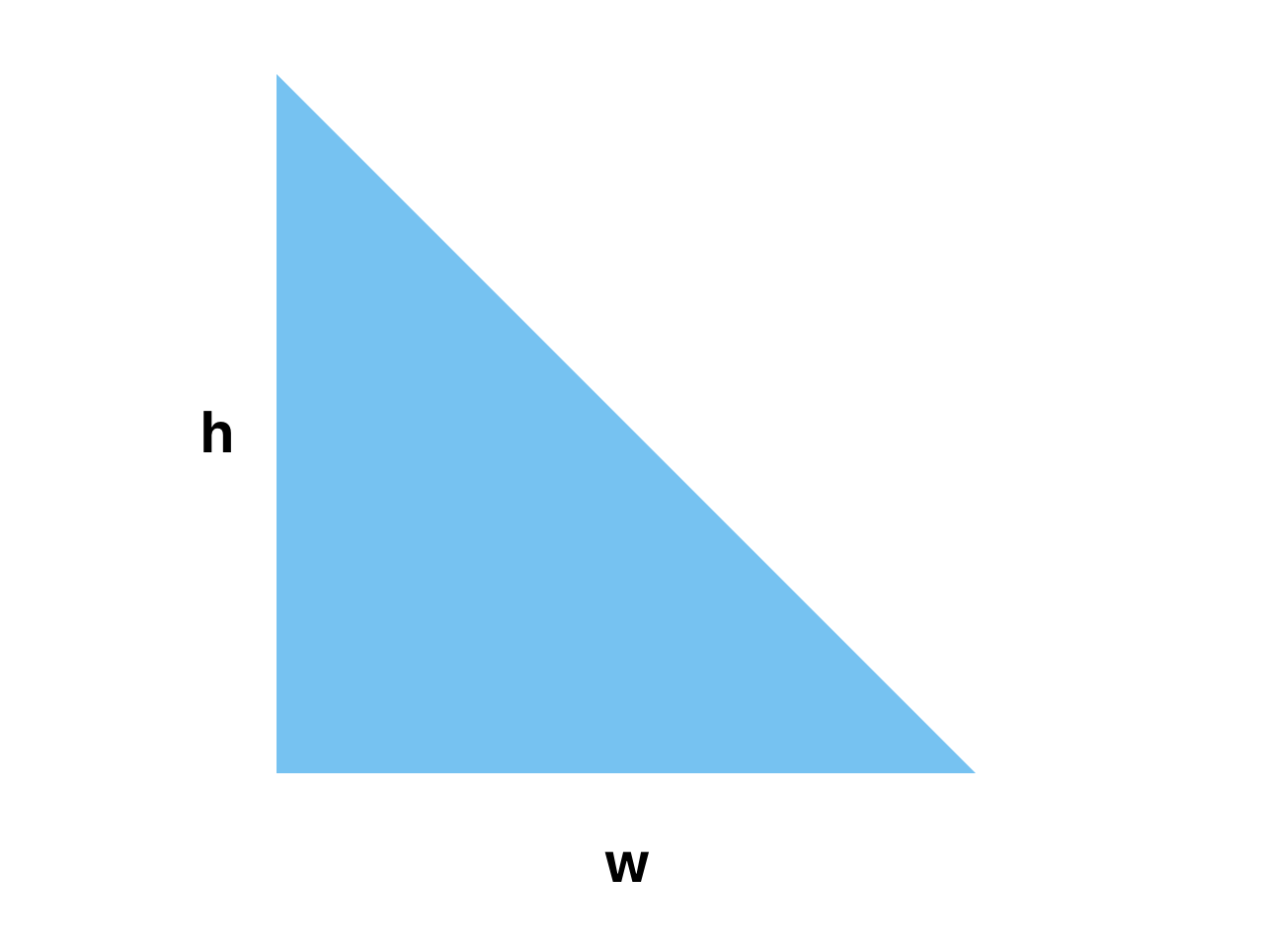
We can divide it into several narrow rectangles. If the width of each rectangle is sufficiently small, the sum of their areas will equal the area of the triangle:

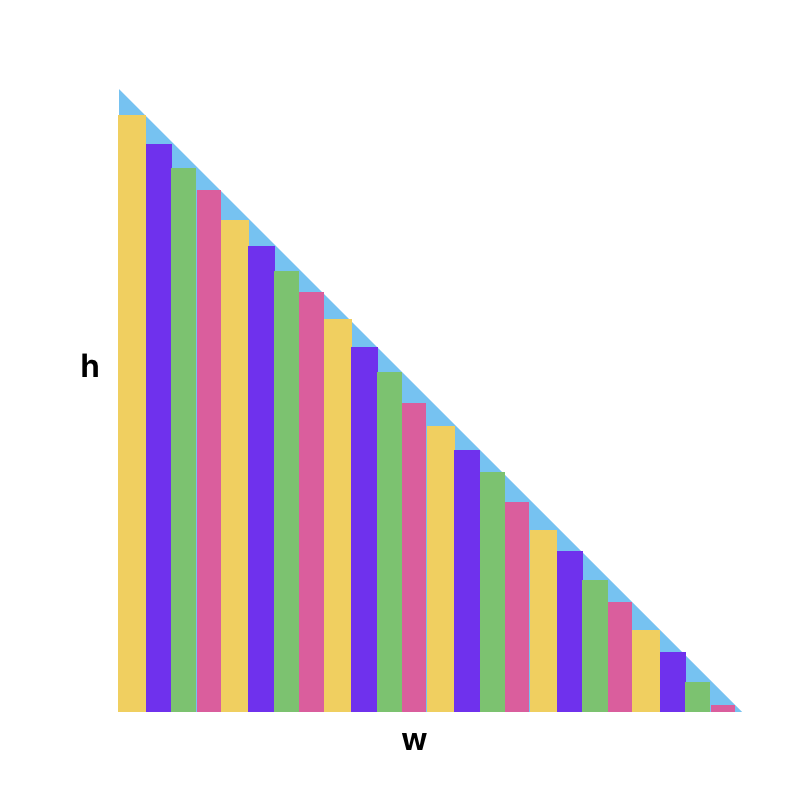
Let’s divide the width into n equal parts:

The height is also divided into n equal parts, with each rectangle on the right being shorter by h / n. We denote this as Δh = h / n :

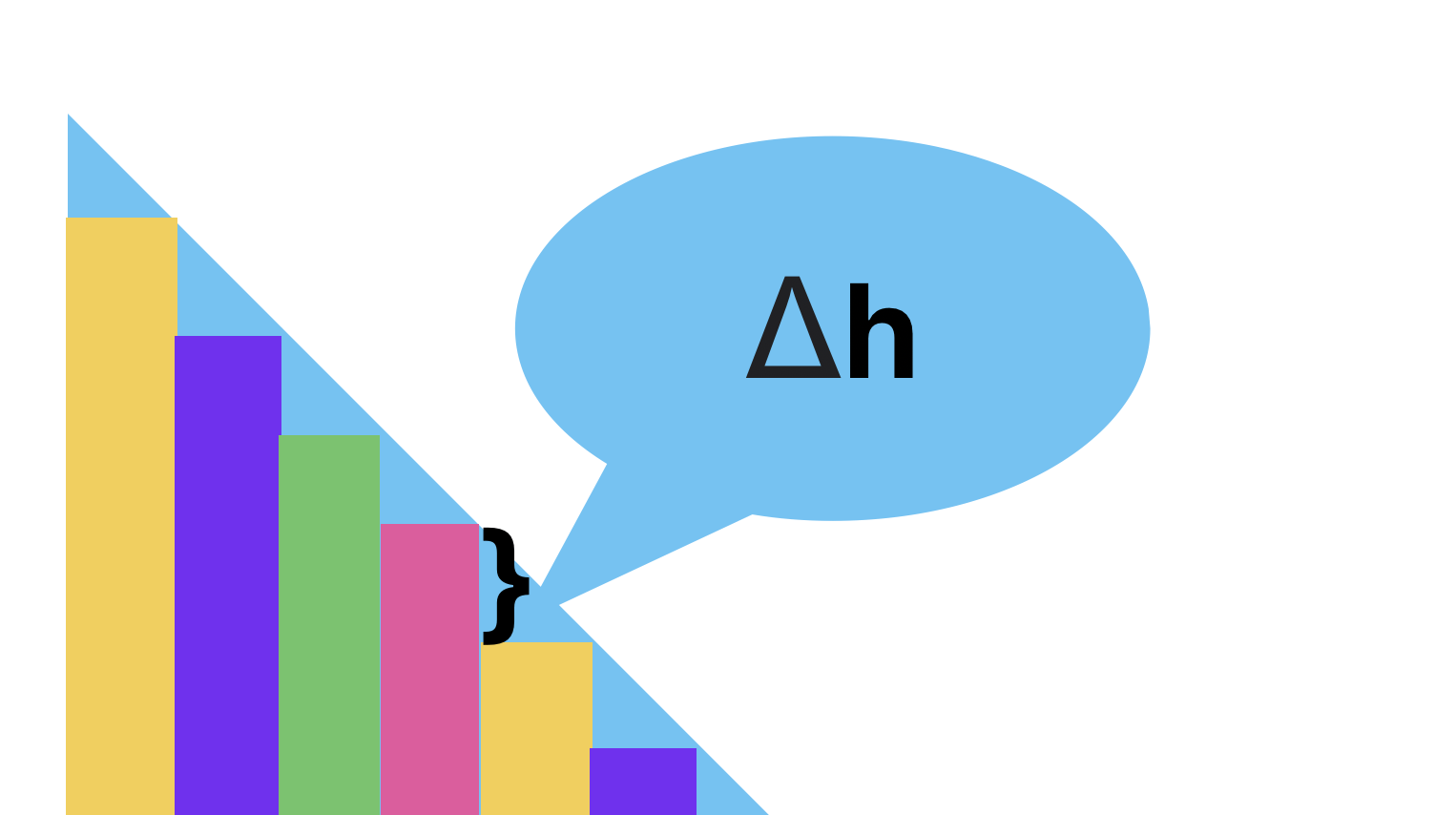
Now, let’s calculate:

• The area of the first rectangle is: S = w/n * h;
• The area of the second rectangle is: S = w/n * (h - Δh);
• The area of the third rectangle is: S = w/n * (h - Δh * 2);
• …
• The area of the n rectangle is: S = w/n * (h - Δh * (n-1)).

We sum them all up:

S = w/n * h + w/n * (h - Δh) + … + w/n * (h - Δh * (n-1))

S = w/n * (h + (h - Δh)+ … + (h - Δh * (n-1)))

S = w/n * (h * n - Δh * (1 + 2 + … + (n-1)))

S = w/n * (h * n - Δh * n * n/2)

Since h = Δh * n, we can further simplify:

S = w/n * (h * n - h * n/2)

S = w/n * h * n/2

S = w * h /2

Thus, we derive the area of the triangle as S = w * h /2.

Isn’t that interesting? Let’s continue.

Circumference of a Circle

Before discussing the area of a circle, let’s talk about its circumference.

I don’t know if you’ve ever done this, but I tried it myself: drawing a circle with a compass, cutting it out from the paper, and measuring its circumference with a tape measure. I found that the circumference is indeed about six times the radius. The larger and more precise your circle, the closer you’ll get to the exact multiple.

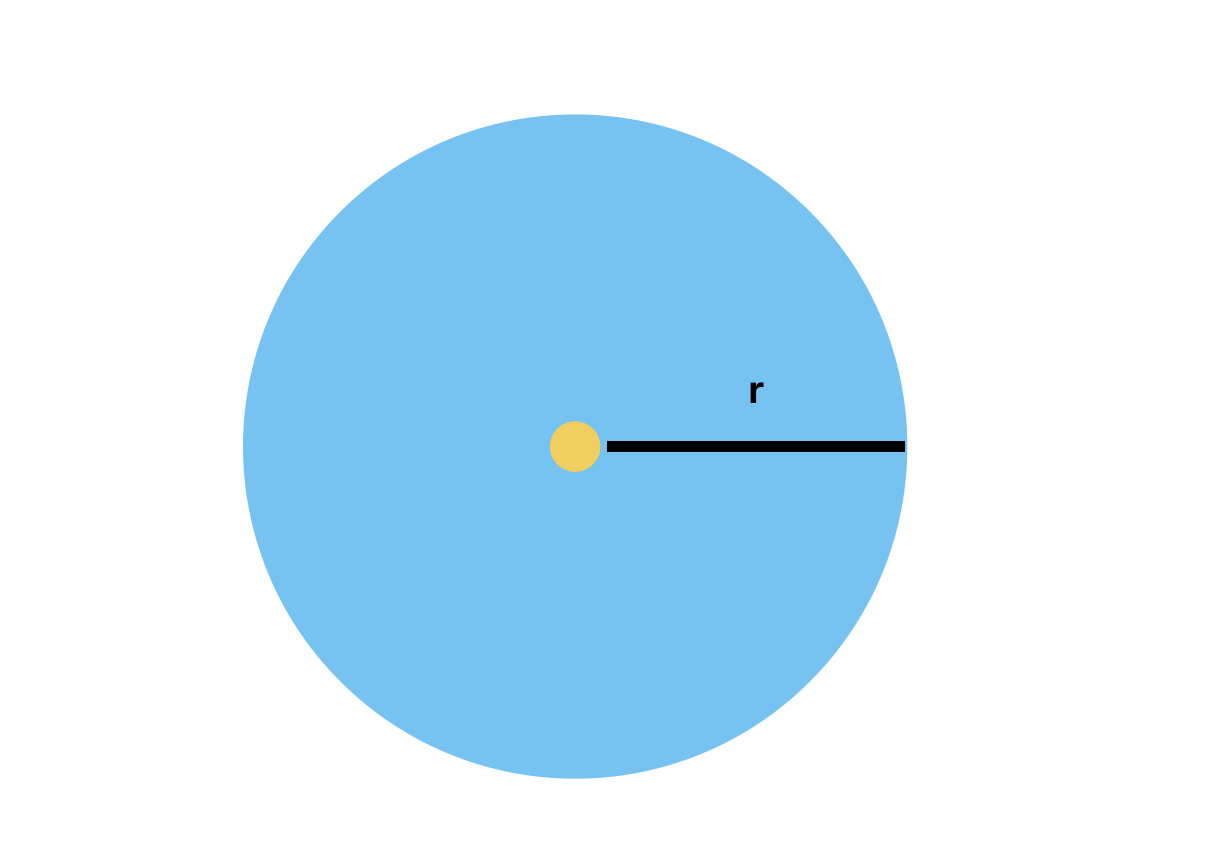
We all know the formula for the circumference of a circle is C = 2 * π * r, which can be practically verified using the method I just described.

Area of a Circle

Using the method we applied to calculate the area of a triangle, we can divide a circle into narrow strips, like this:

We can then rearrange these strips, as shown here:

Does it look familiar? It starts to resemble a triangle.

We divide the circle into n equal-width sections, so each strip has a width of r / n.

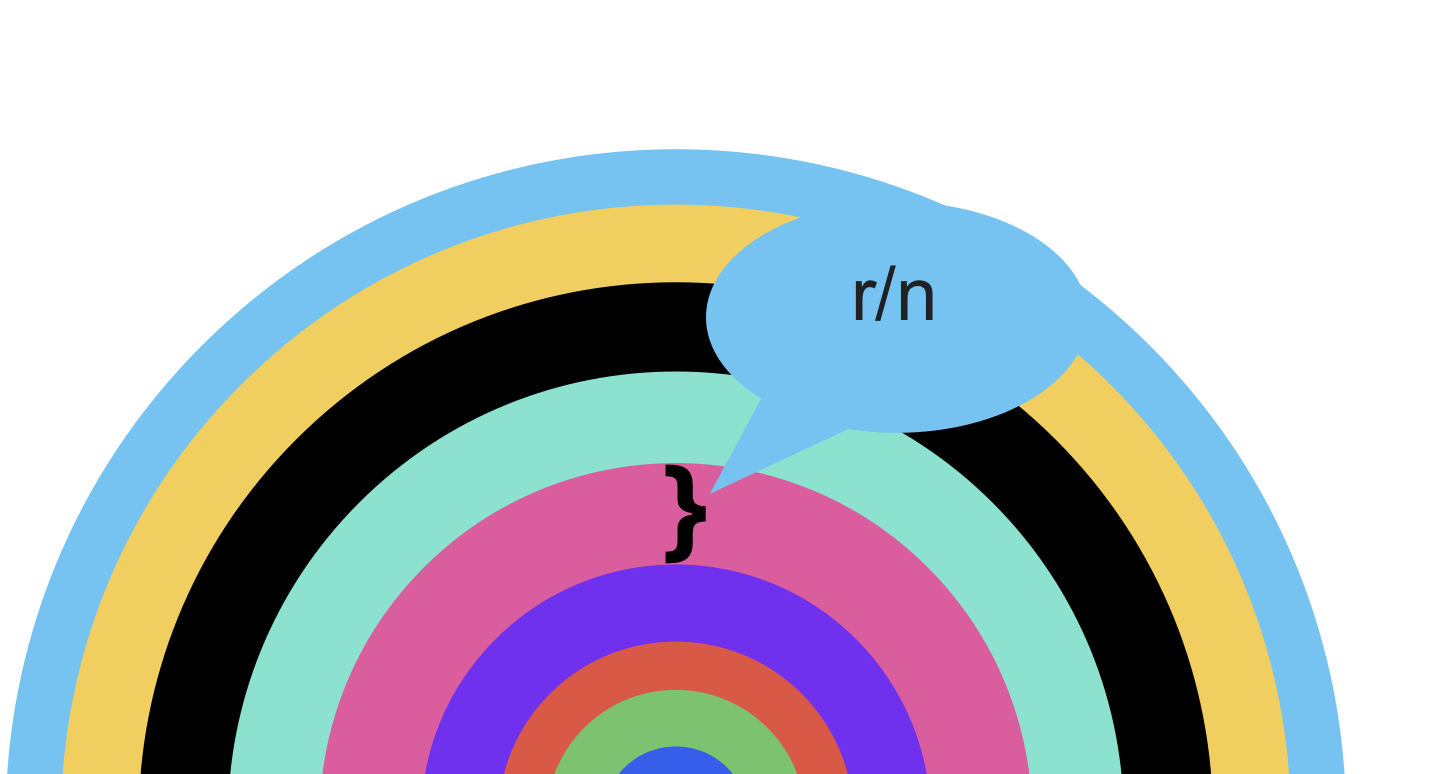
The length of the outermost strip is the circumference of the circle, C = 2 * π * r. In the case of the triangle, this corresponds to the height h of the rectangles, while the total width of all strips equals the radius r.

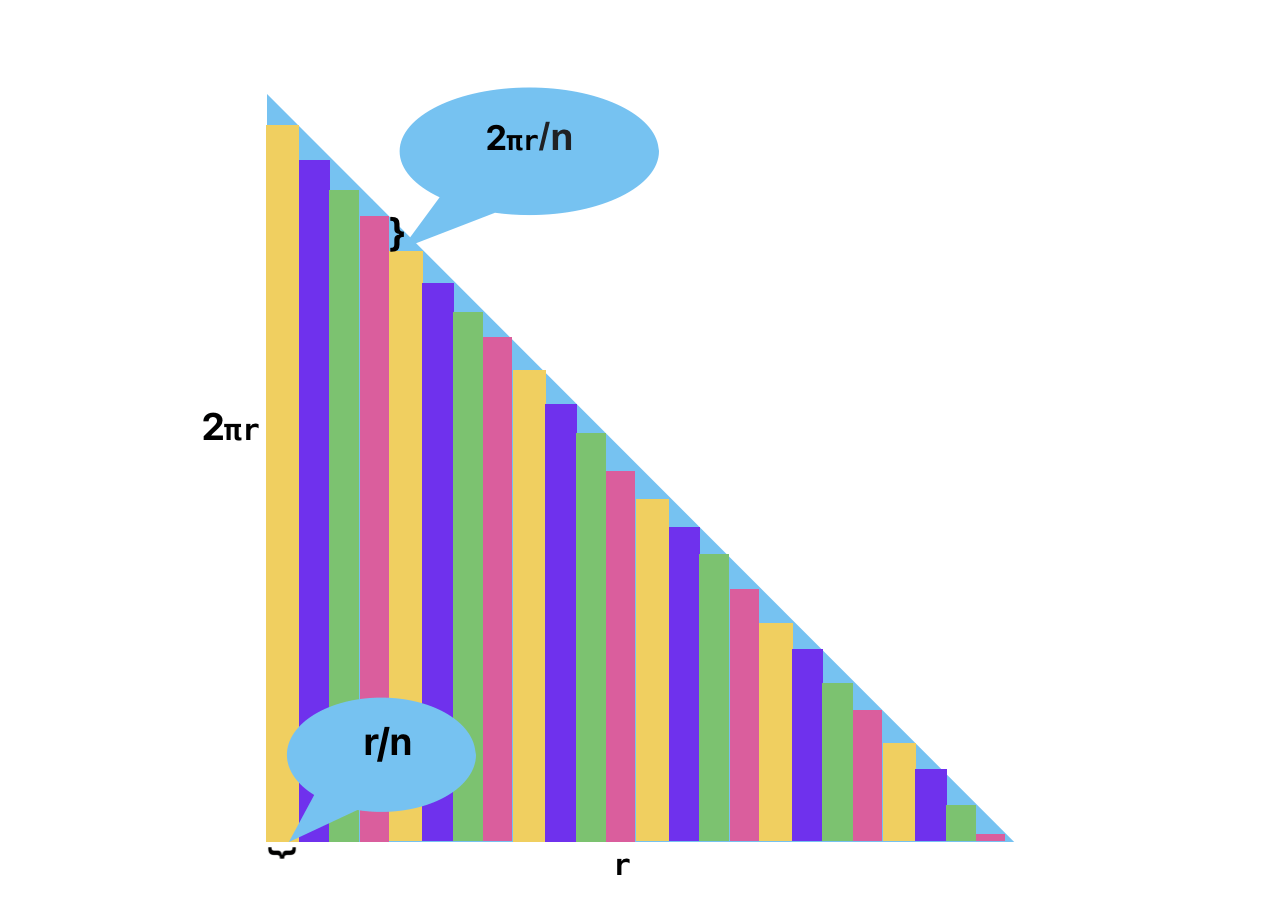
Since it’s now a triangle, we calculate its area using the formula S = w * h /2:

S = w * h /2

S = r * (2 * π * r) /2

S = π * r * r

Thus, we’ve calculated the area of the circle. Isn’t it fascinating?

That’s all for this article. More to come later.